An Introduction To 2s Complement: Its Definition, Conversions, And Examples

In mathematics, the 2s complement is an operation in which the binary variables are involved. The twos complement is widely used in the computer (machine) language to encode and decode computer codes.

It is especially used to determine the 2s complement of negative numbers. While one’s complement is available but it is only applicable for the positive numbers. In this article, we will discuss all the theory and examples of the twos complement.

2s complement

In number system, the 2s complement is an operation that is frequently used to encode the negative and positive numbers in the form of binary variables. It is usually used in logic gates such as AND gate, NOT gate, OR gate, etc.

While the working of 1s complement is almost similar to twos complement but it is only applicable for the positive binary, decimal, & hexadecimal numbers. The reason of creating a new operation is just for the representation of the negative terms.

The 2s complement is a perfect example of true complement (radix complement). Twos complement can be evaluated by adding 1 to the least significant bit of the 1s complement. While the one’s complement is determined by taking the transpose of the binary numbers.

The transformation of various number systems into 2s complements

To turn the binary and decimal numbers system into two’s complement, follow the below procedure.

1. The transformation of Binary numbers into 2s complement

To transform the binary variables into 2s complement, keep an eye on the following steps.

1. Firstly, take a number in the form of 0 & 1.
2. Invert all the binary variables such as transform all the 1s into 0s and all the 0s into 1s. the inversion of the binary variable is said to be the transpose. The process gives you the result of the one’s complement.
3. Add one to the LSB of the transpose of the binary variables.
4. The final result will be the 2s complement of the binary variable.

Now you are able to transform any binary variable into 2s complement just by learning the above steps. A 2’s complement calculator can be used to get the result according to the above steps. Let us take a few examples to learn how to implement these steps manually.

Example - 1

Transform 110011001010 into twos complement.

Solution

Step - 1 : Firstly, take a number in the form of 0 & 1.

110011001010

Step - 2 : Invert all the binary variables such as transform all the 1s into 0s and all the 0s into 1s.

001100110101

Step - 3 : Add one to the LSB of the transpose of the binary variables to get the result in twos complement.

Therefore,

001100110110 is the twos complement of the given binary number.

Example - 2

Transform the given 16-bit binary number into twos complement.

0001110001110001

Solution

Step - 1 : Firstly, take a number in the form of 0 & 1.

0001110001110001

Step - 2 : Invert all the binary variables such as transform all the 1s into 0s and all the 0s into 1s.

0001110001110001

Step - 3 : Add one to the LSB of the transpose of the binary variables to get the result in twos complement.

Therefore,

0001110001110010 is the twos complement of the given binary number.

2. The transformation of decimal numbers into twos complement

To transform the positive and negative decimal numbers into 2s complement, keep an eye on the following steps.

For positive decimal number

1. Firstly, take the positive decimal number in the form of base 10.
2. Transform the given positive base 10 number in the form of base 2 number.
3. Invert all the binary variables such as transform all the 1s into 0s and all the 0s into 1s. the inversion of the binary variable is said to be the transpose. The process gives you the result of the one’s complement.
4. Add one to the LSB of the transpose of the binary variables.
5. The final result will be the 2s complement of the binary variable.

For negative decimal number

1. Firstly, take the negative decimal number in the form of base 10.
2. Then calculate the twos complement of the base 10 number without negative sign by following the above steps.
3. Invert all the binary variables of the twos complement of positive number such as transform all the 1s into 0s and all the 0s into 1s. the inversion of the binary variable is said to be the transpose. The process gives you the result of the one’s complement.
4. Add one to the LSB of the transpose of the two’s complement of positive number.
5. The final result will be the 2s complement of the binary variable.

Now you are able to transform any positive or negative decimal numbers into 2s complement just by learning the above steps. Let us take a few examples to learn how to implement these steps manually.

Example 1: For a positive decimal number

Transform 478 into 2s complement.

Solution

Step - 1 : First of all, take the negative decimal number in the form of base 10.

478

Step - 2 : Now Transform the given positive base 10 number in the form of base 2 number.

Hence,

478 = (111010100)2

Step - 3 : Invert all the binary variables such as transform all the 1s into 0s and all the 0s into 1s.

111010100

Step - 4 : Add one to the LSB of the transpose of the binary variables to get the result in twos complement.

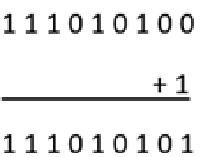
Therefore,

111010101 is the twos complement of the given positive decimal number.

Example 2 : For a negative decimal number

Transform -718 into 2s complement.

Solution

Step - 1 : First of all, take the negative decimal number in the form of base 10.

-718

Let’s calculate the 2s complement of positive 718.

Step - 2 : Now Transform the given positive base 10 number in the form of base 2 number.

Hence,

718 = (1011001110)2

Step - 3 : Invert all the binary variables such as transform all the 1s into 0s and all the 0s into 1s.

0100110001

Step - 4 : Add one to the LSB of the transpose of the binary variables to get the result in twos complement.

Hence,

0100110010 is the 2s complement of 718.

Step - 5 : Now treat the 2s complement of 357 as a binary variable and apply the procedure of binary to 2s complement to determine the 2s complement of the negative decimal number.

1011001101

Step - 6 : Add one to the LSB of the transpose of the binary variables to get the result in twos complement.

Hence,

1011001110 is the 2s complement of - 718.

Wrap up

Now you can easily convert the base 2 number system and base 10 number system into 2s complement just by learning the steps discussed in the above post. You can get all the basics the two’ complement just by learning this post.